This article was written by referring to the Fall 2020 Numerical Analysis: Linear Algebra Course and the following links.

Gram–Schmidt Process

Given a set of linearly independent vectors $Span({ a_0, … , a_{n-1} } ) \subset \mathbb{C}^m$, the Gram-Schimdt process computes a new basis {$q_0, … , q_{n-1}$} that spans the same subspace as the original vectors, i.e. $Span({ a_0, … , a_{n-1} } ) = Span({ q_0, … , q_{n-1} } )$ [1].

It should be noted that we would like to have the new basis, ${ q_0, … , q_{n-1} }$, having the following characteristics.

  • All vectors are unit vectors of length 1, i.e. $|q_i| = 1$.
  • All vectors are mutually perpendicular, i.e. $q_i \perp q_j$ where $i \neq j$.

These characteristics can be obtained through the following routine which is composed by three steps [1]:

<Gram-Schmidt Process>
  Step 1. Compute the direction of the vectors.
  Step 2. Compute the magnitude of the normalizer.
  Step 3. Compute a unit vector.
  • Compute the vector $q_0$ ($i=0$)
    • Step 1. Compute the direction of the vectors.
    \[N.A. \ (q_0 \parallel a_0)\]
    • Stpe 2. Compute the magnitude of the normalizer.
    \[\rho_{0, 0}=\|a_0\|_2\]
    • Step 3. Compute a unit vector.
    \[q_0=a_0/\rho_{0, 0}\]
    • Result
    \[a_0=q_0\rho_{0, 0}\]
  • Compute the vector $q_1$ ($i=1$)
    • Step 1. Compute the direction of the vectors.
    \[\rho_{0, 1}=q_0^{H}a_1\] \[a_{1}^{\perp}=a_1-\rho_{0, 1}q_0\]
    • Step 2. Compute the magnitude of the normalizer.
    \[\rho_{1, 1}=\|a_1^\perp\|_2\]
    • Step 3. Compute a unit vector.
    \[q_1=a_1^\perp/\rho_{1, 1}\]
    • Result
    \[\left[\begin{array}{c|c}a_{0} & a_{1}\end{array} \right]= \left[\begin{array}{c|c}q_{0} & q_{1}\end{array} \right] \left[\begin{array}{c|c} \rho_{0, 0} & \rho_{0, 1} \\ \hline 0 & \rho_{1, 1} \end{array} \right]\]
  • Compute the vector $q_2$ ($i=2$)
    • Step 1. Compute the direction of the vectors.
    \[\begin{bmatrix}\rho_{0, 2} \\ \rho_{1, 2}\end{bmatrix}=\begin{bmatrix}q_{0} & q_{1}\end{bmatrix}^Ha_2\] \[a_{2}^{\perp}=a_2-\begin{bmatrix}q_{0} & q_{1}\end{bmatrix}\begin{bmatrix}\rho_{0, 2} \\ \rho_{1, 2}\end{bmatrix}\]
    • Step 2. Compute the magnitude of the normalizer.
    \[\rho_{2, 2}=\|a_2^\perp\|_2\]
    • Step 3. Compute a unit vector.
    \[q_2=a_2^\perp/\rho_{2, 2}\]
    • Result
    \[\left[\begin{array}{c|c}a_{0} \ a_{1}& a_{2}\end{array} \right]= \left[\begin{array}{c|c}q_{0} \ q_{1} & q_{2}\end{array} \right] \left[\begin{array}{cc|c} \rho_{0, 0} & \rho_{0, 1} & \rho_{0, 2} \\ 0 & \rho_{1, 1} & \rho_{1, 2}\\ \hline 0 & 0 & \rho_{2, 2} \end{array} \right]\]
  • keep do the routine till $i=n-1$
    • Step 1. Compute the direction of the vectors.
    • Step 2. Compute the magnitude of the normalizer.
    • Step 3. Compute a unit vector.
    • Final Result
\[A = QR\]

What we should pay attention to in the final result ($A = QR$) are …

  • All column vectors of $Q$, the new basis {$q_0, … , q_{n-1}$}, are unit vector and mutually orthogonal, which means $Q$ is an unitary matrix.

  • The matrix $R$ is upper triangular matrix and $rank(R)=m$.

  • The dot product of $Q$ and $R$, which is equal to $A$, can be regarded as a linear combination of $Q$’s column vectors.

  • The result of Gram-Shmidt Process can be regarded as a result of QR factorization (decomposotion).


Classical Gram-Schmidt (CGS)

The content discussed in the previous section can be summarized into an algorithm as follows, which is the CGS-QR algorithm [2].

Consider $A=QR$.

Partition the given matrices as follows.

\[\left[\begin{array}{c|cc}A_{0} & a_{1} & A_{2}\end{array} \right]= \left[\begin{array}{c|cc}Q_{0} & q_{1} & Q_{2}\end{array} \right] \left[\begin{array}{c|cc} R_{0, 0} & r_{0, 1} & R_{0, 2} \\ \hline 0 & \rho_{1, 1} & r_{1, 2}^T\\ 0 & 0 & R_{2, 2} \end{array} \right]\]

Assume that $Q_0$ and $R_{0,0}$ have already been computed.

Since $Q$ is unitary matric ($Q_0^HQ_0=I$ and $Q_0^Hq_1=0$),

  • $Q_0^Ha_1=Q_0^HQ_0r_{0,1}+q_1\rho_{1,1}=r_{01}$

Compute $r_{0,1}$, which is already known.

  • $r_{0,1}:=Q_0^Ha_1$

Compute $a_1^\perp$ and $\rho_{1,1}$ (Step 1. & 2.).

  • $a_1^\perp:=a_1-Q_0r_{0,1}$
  • $\rho_{1,1}:=|a_1^\perp|$

Compute $q_1$ (Step 3.).

  • $q_1 := a_1^\perp / \rho_{1,1}$

Figure 1. shows Classical Gram-Schmidt algorithm for computing the QR factorization of a matrix A. The algorithm used FLAME notation.
Code 1. shows the algorithms in python language.

Figure 1. Classical Gram-Schmidt algorithm for computing the QR factorization of a matrix A [2]


Code. 1: CGS QR in python


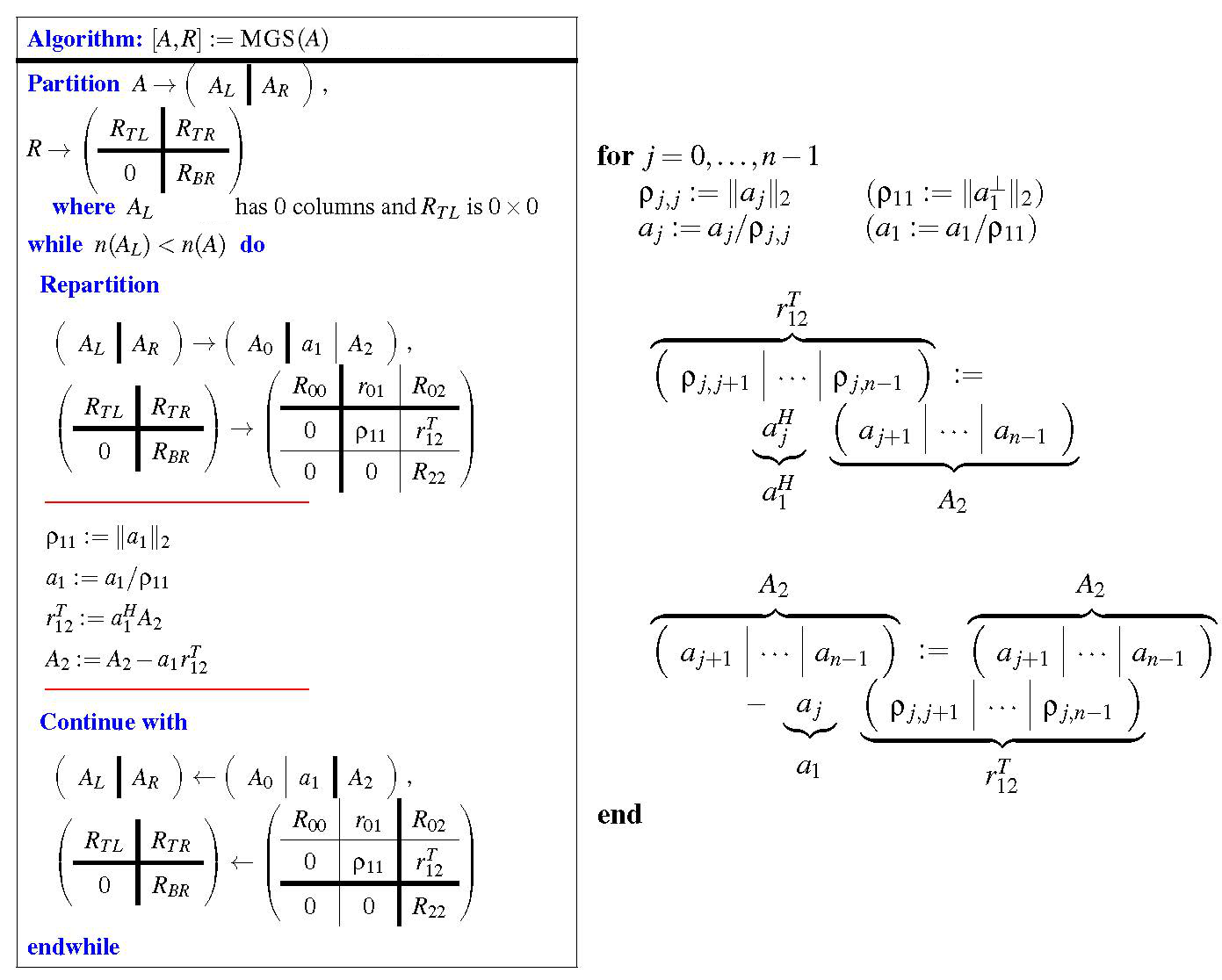
Modified Gram-Schmidt (MGS)

Gram-Schmidt process can be performed differently from CGS, and the corresponding algorithm is as follows, which is called Modified Gram-Schmidt (MGS) [3].

Consider $A=QR$.

Partition the given matrices as follows.

\[\left[\begin{array}{c|cc}A_{0} & a_{1} & A_{2}\end{array} \right]= \left[\begin{array}{c|cc}Q_{0} & q_{1} & Q_{2}\end{array} \right] \left[\begin{array}{c|cc} R_{0, 0} & r_{0, 1} & R_{0, 2} \\ \hline 0 & \rho_{1, 1} & r_{1, 2}^T\\ 0 & 0 & R_{2, 2} \end{array} \right]\]

Assume that $a_1$ and $A_2$ are known.

Compute $\rho_{1,1}$ (compute the magnitude ↔︎ Step 2.).

  • $\rho_{1,1}:=|a_1|$

Compute $q_1$ (compute the unit vector ↔︎ Step 3.).

  • $q_1:=a_1/\rho_{1,1}$

Compute $r_{0,1}^T$, which is already known.

  • $r_{0,1}^T:=q_1^H(A_2 - Q_2R_{22}) = q_1^HA_2$

Compute $A_2$ (update $A_2$ for the orthogonality ↔︎ Step 1.).

  • $A_2:=A_2-q_1r_{0,1}^T$

Figure 2. shows Modified Gram-Schmidt algorithm for computing the QR factorization of a matrix A. The algorithm used FLAME notation.
Code 2. shows the algorithms in python language.

Figure 2. Alternative Modified Gram-Schmidt algorithm for computing the QR factorization of a matrix A [3]


Code. 2: MGS QR in python


Why do we need this?

Through Gram-Schmidt process, we can obtain an orthonormal basis of the matrix $A$’s subspace, which has a set of lineary independent vectors {$a_0, …, a_{n-1}$}.

The advantages of being able to have an orthonormal basis are following [4].

  • We can express any $v \in \mathbb{C}^n$ as a linear combination of coefficients, which will allows us to have an explicit formula expressing $v$ with the orthonormal basis.

  • The explicit formula is very useful when dealing with projection onto subspace.

References

[1] M. M. Robert van de Geijn, “Advanced Linear Algebra: Foundations to Frontiers,” ALAFF Classical Gram-Schmidt (CGS). [Online]. Available: https://www.cs.utexas.edu/users/flame/laff/alaff/chapter03-classical-gram-schmidt.html. [Accessed: 03-Jan-2021].

[2] M. M. Robert van de Geijn, “Advanced Linear Algebra: Foundations to Frontiers,” ALAFF Classical Gram-Schmidt algorithm. [Online]. Available: https://www.cs.utexas.edu/users/flame/laff/alaff/chapter03-cgs-algorithm.html. [Accessed: 03-Jan-2021].

[3] M. M. Robert van de Geijn, “Advanced Linear Algebra: Foundations to Frontiers,” ALAFF Modified Gram-Schmidt (MGS). [Online]. Available: https://www.cs.utexas.edu/users/flame/laff/alaff/Modified-Classical-Gram-Schmidt.html. [Accessed: 03-Jan-2021].

[4] Michael Albanese, “Why is orthogonal basis important?,” Mathematics Stack Exchange. [Online]. Available: https://math.stackexchange.com/questions/518600/why-is-orthogonal-basis-important. [Accessed: 03-Jan-2021].